題 目：基于累積協方差矩陣的多元響應變量的充分降維方法
主講人：周亭攸副教授
時 間：2023年4月20日（周四）14:30-15:30
地 點：6號學院樓500會議室
主辦單位：新葡萄8883官網AMG 浙江省2011“數據科學與大數據分析協同創新中心”
摘 要：
度量和檢驗兩個隨機變量之間的相互依賴關系歷來都是進行統計研究之中的一個基本問題。本文提出了一種新的穩健度量——累積協方差矩陣(Cumulative Covariance Matrix， 簡稱CCM) ——用來檢驗一個p維隨機向量x的條件均值是否依賴于另一個q維隨機向量y。我們首先證明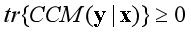
恒成立，并且，當且僅當y的條件均值
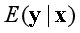不依賴于x時，等號成立。隨后研究其樣本估計量
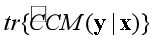的漸近性質并證明：當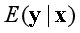不依賴于x時，此樣本估計量是 n相合的; 否則則是根號n相合的。此外，還通過大量的數值模擬說明，基于
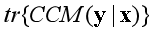的條件均值獨立性檢驗具有良好的大小和功效，并且該優勢在數據中存在極端值時更加顯著。最后，我們基于累積協方差矩陣提出了一種針對多元響應變量的充分降維方法，用來估計中心降維子空間
，并證明了該方法的相合性。該降維方法不用考慮切片，能夠避免多重隨機投影而導致的降維結果的不穩定，并且在響應變量中存在異常值時具有穩健的性質。最后通過廣泛的數值模擬和人體血壓的實際數據分析展示了該降維方法的有限樣本性質。
主講人簡介：
周亭攸，女，1990年生，2017年畢業于上海財經大學統計與管理學院，博士學位?，F任職于新葡萄8883官網AMG，副教授。長期從事統計學理論和方法研究，研究方向集中在高維及超高維數據統計分析、半參數回歸模型統計推斷等領域。
歡迎各位老師和同學積極參加！
